
Zadanie Odtwarzacz MP3 (mp3)
Pomóż nam usprawnić bazę zadań!
Odtwarzacz MP3
Limit pamięci: 256 MB
Grzegorz dostał właśnie odtwarzacz MP3, który ma wiele ciekawych funkcjonalności, a wśród nich blokadę klawiatury.
Jeśli tylko odtwarzacz jest nieaktywny przez ponad\;  sekund, wszystkie jego przyciski zostają zablokowane.
Jeśli blokada klawiatury jest włączona, żaden przycisk nie spełnia swojej normalnej funkcji, a gdy tylko jakikolwiek
przycisk zostaje naciśnięty, blokada zostaje wyłączona.
sekund, wszystkie jego przyciski zostają zablokowane.
Jeśli blokada klawiatury jest włączona, żaden przycisk nie spełnia swojej normalnej funkcji, a gdy tylko jakikolwiek
przycisk zostaje naciśnięty, blokada zostaje wyłączona.
Dla przykładu, załóżmy że 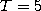 oraz że klawiatura jest aktualnie zablokowana.
Grzegorz nacisnął przycisk
oraz że klawiatura jest aktualnie zablokowana.
Grzegorz nacisnął przycisk  , poczekał 3 sekundy, nacisnął przycisk
, poczekał 3 sekundy, nacisnął przycisk  ,
poczekał 5 sekund, nacisnął
,
poczekał 5 sekund, nacisnął  , poczekał 6 sekund, a następnie nacisnął
, poczekał 6 sekund, a następnie nacisnął  .
W tym przykładzie jedynie przyciski
.
W tym przykładzie jedynie przyciski  oraz
oraz  zadziałały standardowo.
Zauważ, że między naciśnięciami przycisków
zadziałały standardowo.
Zauważ, że między naciśnięciami przycisków  oraz
oraz  włączyła się blokada klawiatury.
włączyła się blokada klawiatury.
Głośność odtwarzacza MP3 kontroluje się za pomocą przycisków + oraz -,
które odpowiednio zwiększają albo zmniejszają poziom głośności o  jednostkę.
Poziom głośności jest liczbą całkowitą między
jednostkę.
Poziom głośności jest liczbą całkowitą między  a
a  .
Naciśnięcie przycisku + przy poziomie głośności
.
Naciśnięcie przycisku + przy poziomie głośności  albo przycisku -
przy poziomie głośności
albo przycisku -
przy poziomie głośności  nie zmienia aktualnej głośności.
nie zmienia aktualnej głośności.
Zadanie
Grzegorz nie zna wartości parametru  . Postanowił wyznaczyć tę wartość eksperymentalnie.
Zaczynając z zablokowaną klawiaturą, wykonał sekwencję
. Postanowił wyznaczyć tę wartość eksperymentalnie.
Zaczynając z zablokowaną klawiaturą, wykonał sekwencję  naciśnięć przycisków + i/lub -.
Na końcu eksperymentu odczytał z wyświetlacza odtwarzacza ostateczny poziom głośności.
Niestety, zapomniał, jaka była głośność odtwarzacza przed rozpoczęciem eksperymentu.
Nieznany, początkowy poziom głośności oznaczmy przez
naciśnięć przycisków + i/lub -.
Na końcu eksperymentu odczytał z wyświetlacza odtwarzacza ostateczny poziom głośności.
Niestety, zapomniał, jaka była głośność odtwarzacza przed rozpoczęciem eksperymentu.
Nieznany, początkowy poziom głośności oznaczmy przez  ,
a znany, ostateczny poziom głośności oznaczmy przez
,
a znany, ostateczny poziom głośności oznaczmy przez  .
.
Masz daną wartość parametru  oraz listę naciśnięć przycisków w takiej kolejności, w jakiej naciskał je Grzegorz.
Dla każdego naciśnięcia znasz typ naciśniętego przycisku (+ lub -)
oraz liczbę sekund od początku eksperymentu do chwili, w której przycisk został naciśnięty.
Twoim zadaniem jest wyznaczenie największej możliwej, całkowitej wartości parametru
oraz listę naciśnięć przycisków w takiej kolejności, w jakiej naciskał je Grzegorz.
Dla każdego naciśnięcia znasz typ naciśniętego przycisku (+ lub -)
oraz liczbę sekund od początku eksperymentu do chwili, w której przycisk został naciśnięty.
Twoim zadaniem jest wyznaczenie największej możliwej, całkowitej wartości parametru  , zgodnej
z wynikiem eksperymentu.
, zgodnej
z wynikiem eksperymentu.
Specyfikacja wejścia
Pierwszy wiersz wejścia zawiera trzy liczby całkowite  ,
,  oraz
oraz
 (
( ) pooddzielane pojedynczymi odstępami.
Każdy z kolejnych
) pooddzielane pojedynczymi odstępami.
Każdy z kolejnych  wierszy zawiera opis jednego naciśnięcia w sekwencji:
znak "+" lub "-" oraz liczba całkowita
wierszy zawiera opis jednego naciśnięcia w sekwencji:
znak "+" lub "-" oraz liczba całkowita  (
( ), oznaczająca liczbę sekund od chwili rozpoczęcia eksperymentu.
Możesz założyć, że chwile naciśnięć są uporządkowane oraz że wszystkie te chwile są różne
(tzn.
), oznaczająca liczbę sekund od chwili rozpoczęcia eksperymentu.
Możesz założyć, że chwile naciśnięć są uporządkowane oraz że wszystkie te chwile są różne
(tzn.  dla każdego
dla każdego  ).
).
Ograniczenia
Możesz założyć, że  oraz
oraz  .
.
W testach wartych łącznie 40 punktów zachodzi  .
.
W testach wartych łącznie 70 punktów zachodzi  .
.
Specyfikacja wyjścia
Jeśli  może być dowolnie duże, wypisz jeden wiersz zawierający słowo "infinity"
(bez cudzysłowów).
może być dowolnie duże, wypisz jeden wiersz zawierający słowo "infinity"
(bez cudzysłowów).
W przeciwnym przypadku wypisz jeden wiersz zawierający dwie liczby całkowite  oraz
oraz  oddzielone pojedynczym odstępem.
oddzielone pojedynczym odstępem.
Wypisane wartości muszą spełniać warunek, że wykonawszy eksperyment z czasem włączenia blokady
 , począwszy od poziomu głośności
, począwszy od poziomu głośności  , otrzymujemy końcowy poziom głośności
, otrzymujemy końcowy poziom głośności  .
Jeśli jest więcej niż jedno rozwiązanie, wybierz to z nich, które maksymalizuje wartość parametru
.
Jeśli jest więcej niż jedno rozwiązanie, wybierz to z nich, które maksymalizuje wartość parametru
 ; jeśli wciąż jest więcej niż jedno rozwiązanie, wybierz to z nich, które
maksymalizuje wartość parametru
; jeśli wciąż jest więcej niż jedno rozwiązanie, wybierz to z nich, które
maksymalizuje wartość parametru  .
.
(Zauważ, że zawsze istnieje co najmniej jedno rozwiązanie:
jeżeli  , to żaden z przycisków nie spełnia swojej normalnej funkcji, więc wystarczy przyjąć
, to żaden z przycisków nie spełnia swojej normalnej funkcji, więc wystarczy przyjąć  ).
).
Przykłady
Dla danych wejściowych:
6 4 3 - 0 + 8 + 9 + 13 - 19 - 24
poprawną odpowiedzią jest:
5 4
Dla  , przyciski spełniają następujące funkcje: odblokuj, odblokuj, +, +, odblokuj, -.
, przyciski spełniają następujące funkcje: odblokuj, odblokuj, +, +, odblokuj, -.
Dla dowolnego  otrzymalibyśmy
otrzymalibyśmy  .
Zauważ, że przykładowe wyjście zawiera największą możliwą wartość parametru
.
Zauważ, że przykładowe wyjście zawiera największą możliwą wartość parametru  .
.
Dla  ostatnie dwa naciśnięcia klawiszy spełnią swoje normalne funkcje, toteż nie będzie możliwe uzyskanie wartości
ostatnie dwa naciśnięcia klawiszy spełnią swoje normalne funkcje, toteż nie będzie możliwe uzyskanie wartości  .
.
Dla danych wejściowych:
3 10 10 + 1 + 2 + 47
poprawną odpowiedzią jest:
infinity
Jeżeli  , to dla dowolnego
, to dla dowolnego  będzie zachodziło
będzie zachodziło  .
.
Autor zadania: Peter Fulla.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English